Simplifying Fractions

It’s a known fact that we can’t compare fractions with unlike denominators – so expanding or simplifying fractions usually gets the job done.

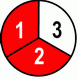
Also often we’ll be simplifying while multiplying and dividing, that really does simplifies things, sometimes even cancels the operation completely. :-)

Concerning converting decimals to fractions, and the decimals being the special form of fractions (it’s all 10ths, 100ths, 1000ths etc) – it’s very common to run into reducing. Simplifying fractions is a very common operation and It is used very much while:

• Comparing fractions
• Multiplying fractions
• Dividing fractions
• Decimal to Fraction Conversion

Here are some examples of simplifying fractions in simplest form:

We have 2 sixths, and by dividing both the numerator and the denominator by 2 – we get 1 third.

	2	÷2	=		1
	6	÷2			3

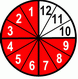
The following one is obvious from the pizza image, but you won’t always get so lucky. You should remember the pattern and then apply it on every case, no matter how complicate it is.

So, 5 tenths (not 5 tents ;-) ), we divide by 5, which is a common factor for 5 and 10, and we get 1 half.

	5	÷5	=		1
	10	÷5			2

There’s another approach to all this. We can factor our numerator and denominator, reduce the common factors - and see what’s left.

	9	=	3 × 3		=		3
	12		4 × 3				4

We see that our common factor for 9 and 12 is 3, so when he is out of the picture – what’s left if our simplified fraction.

Same pattern here. Common factor for 12 and 18 is 6, we "cancel" the 6 – and we have our reduced fraction.

	12	=	2 × 6		=		2
	18		3 × 6				3

Let’s see some "juicy" examples, and this time without pizza images.

90	=	9 × 10	=	3 × 3 × 10	=	3
240		24 × 10		8 × 3 × 10		8

We gradually factor our numbers and stop when we notice the same factors above and below. We can see that we don’t always need to factor down to prime numbers.

168	=	84 × 2	=	42 × 2 × 2	=	7 × 6 × 2 × 2	=	7
120		12 × 10		6 × 2 × 5 × 2		5 × 6 × 2 × 2		5

So, what do we see above? We factor our numerator and denominator, reduce the same factors, and what’s left is our simplified fraction.

Factoring simplifies the procedure very much, so it wise to spend some time practicing this skill.

Conclusion for simplifying fractions section: Fractions with same value are called equivalent fractions If we want to simplify fractions – we have to divide both numerator and denominator with the same number Alternative would be to factor our numerator and denominator and then reduce by canceling the same factors. If we want to "complicate" or expand fractions – we have to multiply both numerator and denominator with the same number

---

Go from Simplifying Fractions to Math Help With Fractions Go from Simplifying Fractions to Free Math Help Online - Home Page