Math Help With Fractions

Hi, I guess you need some math help with fractions. OK, let’s begin this learning fractions journey.

Before we jump into solving fraction problems, we'll go one step at the time.

Obviously first you got to figure out how to recognize, expand and simplify, then to compare them (bigger/smaller/same), to finally operate them.

After all that math help with fractions 101, we'll dig into 4 basic operations, and throw some conversion to decimals and vice versa on the side.

Here's what you can find on this page: What are fractions? Types of fractions Simplifying fractions Expanding fractions Comparing fractions Adding fractions Adding fractions with like denominators Adding fractions with unlike denominators Subtracting fractions Subtracting fractions with like denominators Subtracting fractions with unlike denominators Multiplying fractions Dividing fractions Conversion: Fraction to Decimal Conversion Decimal to Fraction Conversion Convert Fraction to Percent

---

What are Fractions?

Well, fractions are... let’s just say for start that they are (a way of representing) the parts of a whole.

Whole numbers are a "whole" different story – they are whole. ;-) But here we are taking scissors and knives and we cut, divide, chop and slice (in equal parts) and we’re dealing with chunks, parts, slices and pieces.

Every fraction has a numerator, denominator and a horizontal divider line between them.

Let's start this math help with fractions section with red pizza pies and work our way to numbers:

• Numerator (above the line) = number of leftover "pizza slices"
• Denominator (under the line) = number of "pizza slices" "before eating"
• Line represents division, (so 4/2 = 4÷2 = 2)

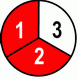
In the following case we’ve divided pizza into 3 slices and ate 2, so we’re left with just ONE THIRD of pizza:

	=		1		Numerator
			3		Denominator

And this, my friends, is a FRACTION! :-D

• 1 is the numerator (red leftover), and
• 3 is the denominator (number of slices before eating, but after slicing)

Now what would you say about this one?

	=		3		Numerator
			4		Denominator

In this case mom and dad bought one big pizza for their four children. But only one kid was hungry (?!) at the moment and ate only 1 slice – so dad decided to provide some math help with fractions and asked the children how many "leftover" slices there are, and the children said – three fourths (or three quarters).

So:

• 3 is the numerator (red leftover), and
• 4 is the denominator (there were 4 pieces before eating)

Although we can represent whole numbers through fractions, we can’t always do the other way around.

For example, if we write 2/2, we could also write it down as 1, because we know 2 ÷ 2 = 1.

			=
	2		=		1	= 1
	2				1

Same goes for any other case.

	3		=		4		=		5		=		6
	3				4				5				6

Reminder: the line represent division.

Whole circle is red so it does not matter on how many parts we cut our pizza. Nothing changes with the total "amount" of pizza while we cut it (something happens only when we eat it. ;-) )

Here, this is number 2 represented as a fraction in several variants:

	6		=		8		=		10		=		12
	3				4				5				6

And now for number 3:

	9		=		12		=		15		=		18
	3				4				5				6

Well, I guess it’s enough, you get the picture. We could go on and on...

On the other hand if we had 1/2, then we couldn’t convert it into a whole number (though we could convert it into a decimal number: 0.5 = five tenths = 5/10, or to percents 50 %).

	=		1		Numerator
			2		Denominator

So one half remains one half = a fraction (a half of 1 whole).

To digress, if you ask me, decimal numbers and percents are only the other, we could say special, form of fractions. Although it may not seem at first – they actually are. The first value on the right to the dot represent the tenths, the second the hundredths (percents represent only the 100ths) – and these all are parts = fractions of a whole. But that’s a whole different story, since this is math help with fractions only. :-)

---

Types of Fractions?

Anyway, there are three types of fractions:

• proper,
• improper and
• mixed

	2	<1		5	≥1	1	2	≥1
	3			3			3
Proper fraction			Improper fraction			Mixed fraction

Proper fraction is every fraction that has a denominator greater than its numerator, or if you like, has a less than 1 value.

Improper and mixed fractions are twins per se. Those are fractions that have value greater than 1.

Then it’s just the matter of which form suits your case better (usually if you plan to do some other operation – improper fraction form is your bet).

Conclusion for math help with fractions section: Every fraction has: Numerator – how many parts we have Denominator – what are those parts (halves, thirds, quarters…) Line – represents division Parts of one singe fraction must be equal There are proper, improper and mixed fractions: Proper fraction is less than 1 (whole number) Improper and Mixed fractions are greater than 1 (whole number) Every improper fraction can be represented as mixed fraction, and vice versa

---

We hope this math help with fractions section provided you with enough basic info for start. This is a new page, and it's about to grow much bigger. :-)

Return from Math Help With Fractions to Free Math Help Online - Home Page