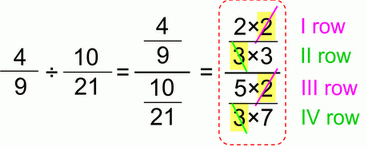|
Dividing Fractions
Loading
How to divide fractions?
No big deal, if you’re already familiar with multiplying fractions – then dividing fractions won’t be a problem. Process of multiplying and dividing fractions is actually very similar. We could say division of fractions is literary one step away from multiplying.
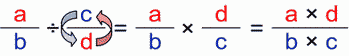
If we switch the numerator/denominator places of the second (divisor) fraction – we get good old multiplication. Let’s examine the following cases: Dividing whole numbers by fractions:
Now, the other way around. Dividing fractions by whole numbers:
Dividing fractions (by fractions):
Before we start with dividing fractions, it’s important for you to:
Dividing whole numbers by fractions
We’re actually dividing whole numbers written in fraction form. Of course, we reduce the yellow highlighted common factors. We can see that the numerator of the divisor (second) fraction ends up below, in the “division area”.
The question for this case would be: if a 4 is one half, how much would be the whole thing? We see that the denominator of the divisor (second) fraction ends up above, in the “multiplication area”.
Again we factored 4 to 2×2 to reduce it with the 2 below. No point in multiplying and dividing by the same number.
Dividing fractions by whole numbersLet’s use the same fractions from the previous 3 examples but we them, but change the place of divisor and dividend. Because of that, we’ll get the reciprocal values to those of previous 3 examples.
Dividing fractions (by fractions)
This is what should you write down if someone would ask you something like this: “if a 1/2 is a 1/3 of some number, what would that number be?” (or something like that).
The remaining numbers are primes, i.e. can’t be factored, so we just multiply.
First we have to turn our mixed fractions into improper ones.
After that we go down the same road as before:
We eliminated the common 7… And finally:
Complex fractionsIn a case of a complex fraction we have the same story:
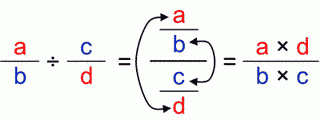
The product of outer (red) numbers (“a” and “d”) is going above as the quotient numerator, and the product of inner (blue) numbers (“b” and “c”) is going below as the quotient denominator.
If the above was simplifying, now follows further solving, i.e. multiplying:
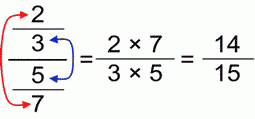
Therefore, we only aren’t allowed to reduce outer and inner “multiplication rows”.
At the end here are the 2 examples on how to turn “incomplete” complex fractions into complete ones. There are usually 3 lines in complex fractions, and if there are 2, we must input the third in there somewhere. We must always be aware of the main line (in the middle), that’s the one in line with an equal sign (wow, this rhymes).
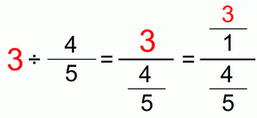
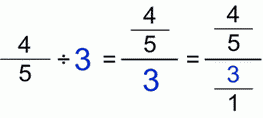
And that's it. If you'd like some more - drop me a line... :-)
|