|
Decimal to Fraction
|
|||||||||||||||||||||||||||||||||||||||
 |
= |
 |
||||
| 0.8 = | 8 | ÷2 | = | 4 | ||
| 10 | ÷2 | 5 | ||||
So, no whole numbers, just 8 10ths. Afterwards we can reduce of course.
Now let’s see a greater-than-one example again with 1 decimal place.
  .
. |
= |
 
 |
|||
|
2.3 = 2 |
3 | = | 2×10 + 3 | = | 23 |
| 10 | 10 | 10 | |||
A point (dot) is a separation point between whole numbers part on the left and the fractions part (10ths, 100ths, 1000ths etc) on the right hand side.
This example, 2 wholes and 3/10, is represented by 2.3.
We notice that there are no 10ths stated anywhere. That’s because they are already implied.
Here’s a shorter (recommended) version for this conversion:
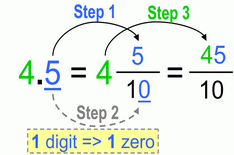
Only 1 decimal place (digit) – means we’re dealing with 10ths, so 1 zero in the denominator (apart from mandatory 1), and then you just lift the whole number (number 4 in this case) up to the numerator.
Now with 2 decimal places:
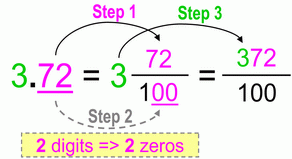
Again, very similar, we have 2 decimal places – that means we’ll have 2 zeros in our denominator. At the end – we lift up the whole number and join it with decimal/fraction part.
It doesn’t matter how big the number is – you always follow the same pattern.
Let’s demonstrate it one more time, now a 2 digit number with 3 decimal places:
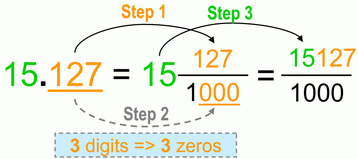
After this fast conversion, we simplify if applicable.
|
Conclusion
|
|
Go from Decimal to Fraction Conversion to Math Help With Fractions Go from Decimal to Fraction Conversion to Free Math Help Online - Home Page |





