Convert
Fraction to Percent

Well, before you see how to convert fraction to percent, I ask you to look at our fraction to decimal conversion page, since this converting to percents is only a sub-case of it, so this is a highly recommended intro to all this.

When we say we want to convert fraction to decimal, more true would be to say that we’re converting from a regular fraction form to a specific fraction (or even a decimal) form. Yup, I’m right, don’t Google it. ;-)
OK, let's see how to convert fraction to percent...

In a nutshell:
We have to turn our fraction’s denominator into 100ths one way or another. As with converting fractions to decimals, we can try to get 100ths by:

• simplifying fractions
• expanding fractions
• dividing the numerator by the denominator

So our converting process would be: Fraction => Fraction (100ths) => Percent, or Fraction => Decimal => Percent

Well, as I’ve said before, decimal numbers are a special form of fractions. We know that decimal numbers are a way of representing whole numbers and its parts in 10ths, 100ths, 1000ths etc (i.e. in 10 based system).

Having said that, percents are fractions with denominator = 100. So, with percents, we’re dealing with 100ths only. Or if we want to say it in decimal terms: only two decimal places after the decimal point count as percents (the rest would be its fraction parts).

Know this: every percent can be represented as a fraction, and vice versa.

Since talk without examples is obscure, let’s offer some convert fraction to percent examples. :-)

---

We’ll start with:

Fraction – Fraction 100ths – Percent
Conversion

Check out this very easy, but illustrative example:

			=				=
	1	×5	=		5	= 0.5	=		50	= 50%
	2	×5			10				100
Fraction				Decimal				Percent

In this particular case, we found a way to get 10ths, and 100ths by expanding of fractions.

As you can see above – these are all fractions. The sizes of parts (denominators) are different, but still fractions. And yet the first one is a regular fraction, the second one is a decimal fraction, and the third one is represented as a percent fraction.

Their total values are the same, so these fractions are also equivalent.

We can also see that regular fractions have no "restrictions" concerning denominators, while decimals are "restricted" to 10s (100s, 1000s etc), and percents nailed to 100ths only (btw, 1$ = 100 cents, so per-cents are 100ths). :-)

Let’s see an another example how to convert fraction to percent.

			=
	3	×25	=	75	= 0.75	= 75%
	4	×25		100
Fraction					Decimal	Percent

In this case we got 100ths right away and there was our percent. Let me repeat, the first two decimal places after the decimal point represent percents.

In this third example let’s have 17/20. Don't let 17 scare you, we’re only interested in getting the 100ths in the denominator – so we expand our 20ths by 5. Since we got our 100ths – our percent is the numerator = 85.

			=
	17	×5	=	85	= 0.85	= 85%
	20	×5		100
Fraction					Decimal	Percent

Useful digression: Decimal Percent   0.3 30%     0.08 8%     0.52 52%     0.453 45.3%     0.0741 7.41%     2.13 213%

---

Now let’s look at those 3 cases from another perspective:

Fraction – Decimal (2 places) – Percent
Conversion

This is classic division, regular division of whole numbers.

We can’t divide 1 by 2 and get a whole number Therefore we represent 1 as 10/10 and then divide by 2 2 goes 5 times into 10 (actually we got 5/10), no remainder We must place that 5 at its appropriate place for 10ths (first place after the decimal point) we also know that we can expand: 5/10 = 50/100 and since percents are above 100ths, our solution is 50%

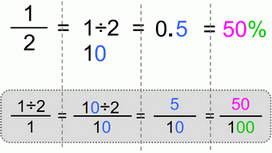
Now let’s see example number 2.

We can’t divide 3 by 4 and get a whole number, Therefore we represent 3 as 30/10 and then divide by 4 4 goes 7 times into 30 (4×7 = 28 < 30), with 2/10 remaining We must place that 7 (7/10) at its appropriate place for 10ths (first place after the decimal point) The remaining 2/10 can’t be divided by 4 Therefore we expand 2/10 into 20/100 and then divide by 4 4 goes 5 times into 20, so we wrap up with 5/100, no remainder So we have 70/100 + 5/100 = 75/100, and since percents are above 100ths, our solution is 75%

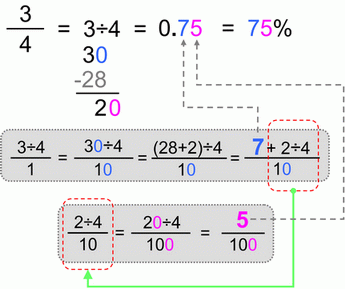
And finally example number 3.

We can’t divide 17 by 20 and get a whole number, Therefore we expand 17 to 170/10 and then divide by 20 20 goes 8 times into 170 (20×8 = 160 < 170), with remaining 10/10 We’re placing that 8 (8/10) at its appropriate place for 10ths (first place after the decimal point) The remaining 10/10 can’t be divided by 20 Therefore we expand 10/10 into 100/100 and then divide by 20 20 goes 5 times into 100, so we end up with 5/100, no remainder Finally we have 80/100 + 5/100 = 85/100, and since percents are above 100ths, our solution is 85%

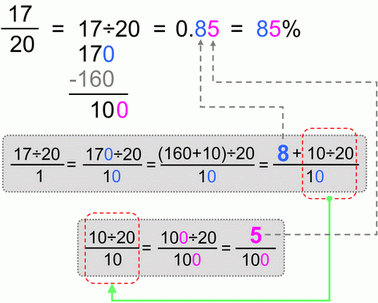
So, that should be enough for starters. Again, if you’d like more convert fraction to percent examples – let me know. Although it would probably be more wise if I’d create some convert fraction to percent worksheets... Bye, bye. Don’t be a stranger. :-)

---

Go from Convert Fraction to Percent to Math Help With Fractions Go from Convert Fraction to Percent to Free Math Help Online - Home Page